1631. 最小体力消耗路径
1631. 最小体力消耗路径
难度中等
你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ,其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ,且你希望去最右下角的格子 (rows-1, columns-1) (注意下标从 0 开始编号)。你每次可以往 上,下,左,右 四个方向之一移动,你想要找到耗费 体力 最小的一条路径。
一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。
请你返回从左上角走到右下角的最小 体力消耗值 。
示例 1:
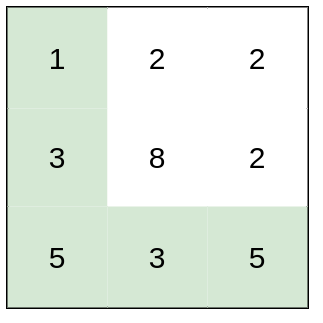
输入:heights = [[1,2,2],[3,8,2],[5,3,5]]
输出:2
解释:路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优,因为另一条路径差值最大值为 3 。示例 2:
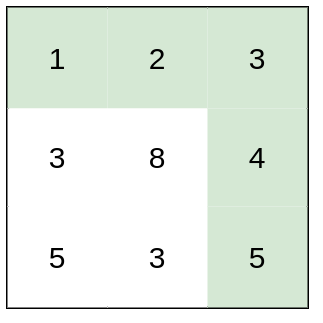
输入:heights = [[1,2,3],[3,8,4],[5,3,5]]
输出:1
解释:路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ,比路径 [1,3,5,3,5] 更优。示例 3:
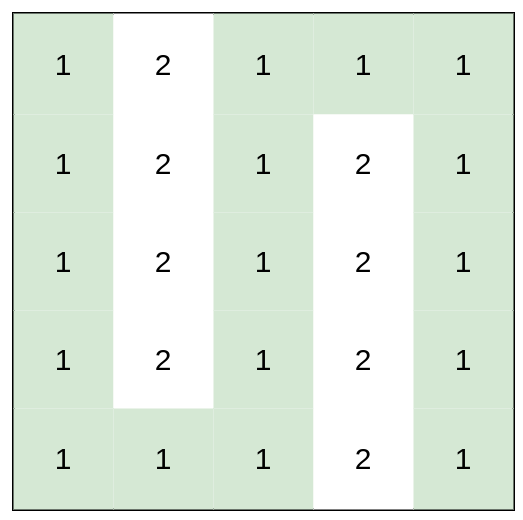
输入:heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出:0
解释:上图所示路径不需要消耗任何体力。提示:
rows == heights.lengthcolumns == heights[i].length1 <= rows, columns <= 1001 <= heights[i][j] <= 10^6
函数签名:
func minimumEffortPath(heights [][]int) int分析
和 《水位上升的游泳池里游泳》 非常类似。
实际可以把每个格子看成图里的顶点,相邻格子可以连一条边,高度差绝对值最为边的权值。问题就是求最短路径。
二分
因为 1 <= heights[i][j] <= 10^6,所以结果在闭区间 [0, 10^6] 内,可以用二分法。
每次指定一个限制值 limit,用 bfs 或 dfs 的方法看看在该限定下能否从起点走到终点。
如下是二分法+bfs的写法:
var dirs = [][]int{ {1, 0}, {-1, 0}, {0, 1}, {0, -1} }
func minimumEffortPath(heights [][]int) int {
m, n := len(heights), len(heights[0])
bfs := func(limit int) bool {
seen := genMemo(m, n)
q := list.New()
q.PushBack([]int{0, 0})
seen[0][0] = true
for q.Len() > 0 {
cur := q.Remove(q.Front()).([]int)
curR, curC := cur[0], cur[1]
if curR == m-1 && curC == n-1 {
return true
}
for _, d := range dirs {
r, c := curR+d[0], curC+d[1]
if r >= 0 && r < m && c >= 0 && c < n &&
!seen[r][c] && abs(heights[r][c]-heights[curR][curC]) <= limit {
seen[r][c] = true
q.PushBack([]int{r, c})
}
}
}
return false
}
return sort.Search(1e6, func(i int) bool {
return bfs(i)
})
}
func abs(x int) int {
if x < 0 {
return -x
}
return x
}
func genMemo(m, n int) [][]bool {
res := make([][]bool, m)
for i := range res {
res[i] = make([]bool, n)
}
return res
}二分法+dfs:
func minimumEffortPath(heights [][]int) int {
m, n := len(heights), len(heights[0])
var dfs func(r, c, limit int, seen [][]bool) bool
dfs = func(curR, curC, limit int, seen [][]bool) bool {
if curR == m-1 && curC == n-1 {
return true
}
seen[curR][curC] = true
for _, d := range dirs {
r, c := curR+d[0], curC+d[1]
if r >= 0 && r < m && c >= 0 && c < n && !seen[r][c] &&
abs(heights[r][c]-heights[curR][curC]) <= limit {
if dfs(r, c, limit, seen) {
return true
}
}
}
// 这里不能把 seen[curR][curC] 重置为 false:
// 如果(curR, curC) 点能在 limit 限制下到达终点会返回 true,不能到达会返回 false,后边也不用再来尝试这个点
return false
}
return sort.Search(1e6, func(i int) bool {
return dfs(0, 0, i, genMemo(m, n))
})
}时间复杂度 O(mnlogC),其中 C 指最大的格子高度,空间复杂度 O(mn)。
借助堆的 bfs
可以只要一次 bfs,每次出队时挑选值最小的元素,这样需要把队列改成小顶堆。
这实际上是求单源最短路径的 Dijkstra 算法。
type Info struct{ r, c, val int }
type Heap struct{ s []Info }
func (h *Heap) Len() int { return len(h.s) }
func (h *Heap) Less(i, j int) bool { return h.s[i].val < h.s[j].val }
func (h *Heap) Swap(i, j int) { h.s[i], h.s[j] = h.s[j], h.s[i] }
func (h *Heap) Push(x interface{}) { h.s = append(h.s, x.(Info)) }
func (h *Heap) Pop() interface{} {
r := h.s[len(h.s)-1]
h.s = h.s[:len(h.s)-1]
return r
}
func (h *Heap) push(x Info) { heap.Push(h, x) }
func (h *Heap) pop() Info { return heap.Pop(h).(Info) }
var dirs = [][]int{ {1, 0}, {-1, 0}, {0, 1}, {0, -1} }
func minimumEffortPath(heights [][]int) int {
m, n := len(heights), len(heights[0])
visited := genMemo(m, n)
h := &Heap{s: make([]Info, 0, m*n)}
h.push(Info{r: 0, c: 0, val: 0})
for h.Len() > 0 {
cur := h.pop() // choose the path whose effort is minimum
if cur.r == m-1 && cur.c == n-1 {
return cur.val
}
if visited[cur.r][cur.c] {
continue
}
visited[cur.r][cur.c] = true
for _, d := range dirs {
r, c := cur.r+d[0], cur.c+d[1]
if r >= 0 && r < m && c >= 0 && c < n && !visited[r][c] {
effort := abs(heights[cur.r][cur.c] - heights[r][c])
h.push(Info{r: r, c: c, val: max(cur.val, effort)})
}
}
}
return -1
}
func max(a, b int) int {
if a > b {
return a
}
return b
}时间复杂度 O(mnlogC),空间复杂度 O(mn)。
注意标记 visited 的时机,不能是入堆的时候,而是出堆的时候。这和《水位上升的游泳池里游泳》不一样,在那个问题在哪个时机入堆都行,且入堆时标记效率更高。
需要画图理解下这两个问题在这里的不同。
[[1,2,2], [3,8,2], [5,3,5]]题目中这个示例为例,如果在入堆的时候就记录,最终路径会是
1,2,2,2,5即先右到头再向下到终点;这个显然是错的。换成在出堆时再记录,最终路径会是
1,3,5,3,5即先向下到底再向右到终点。上边的区别可以类比前序遍历和后序遍历。 也可以扩展备忘录的含义,不单纯记录是否选择了某个格子,而是记录之前访问该格子得到的结果。这样可以改写成先序遍历。
func minimumEffortPath(heights [][]int) int {
m, n := len(heights), len(heights[0])
memo := genMemo(m, n)
h := &Heap{s: make([]Info, 0, m*n)}
h.push(Info{r: 0, c: 0, val: 0})
memo[0][0] = 0
for {
cur := h.pop()
if cur.r == m-1 && cur.c == n-1 {
return cur.val
}
if memo[cur.r][cur.c] < cur.val {
continue
}
for _, d := range dirs {
r, c := cur.r+d[0], cur.c+d[1]
if r < 0 || r >= m || c < 0 || c >= n {
continue
}
effort := max(cur.val, abs(heights[cur.r][cur.c]-heights[r][c]))
if effort < memo[r][c] {
memo[r][c] = effort
h.push(Info{r: r, c: c, val: max(cur.val, effort)})
}
}
}
}func genMemo(m, n int) [][]int {
res := make([][]int, m)
for i := range res {
res[i] = make([]int, n)
for j := range res[i] {
res[i][j] = math.MaxInt64
}
}
return res
}并查集
可以将所有边排序,再一一按边合并所有点,直到起点和终点联通。借助并查集来简化实现。
var uf []int
func find(x int) int {
for x != uf[x] {
x, uf[x] = uf[x], uf[uf[x]]
}
return x
}
func union(x, y int) {
x, y = find(x), find(y)
if x == y {
return
}
uf[x] = y
}
func isConnected(x, y int) bool {
return find(x) == find(y)
}
func minimumEffortPath(heights [][]int) int {
m, n := len(heights), len(heights[0])
type Edge struct {
a, b, val int
}
edges := make([]Edge, 0, m*n*2)
for r, row := range heights {
for c, h := range row {
id := r*n + c
if r > 0 {
edges = append(edges, Edge{a: id, b: (r-1)*n + c, val: abs(h - heights[r-1][c])})
}
if c > 0 {
edges = append(edges, Edge{a: id, b: r*n + c - 1, val: abs(h - heights[r][c-1])})
}
}
}
sort.Slice(edges, func(i, j int) bool {
return edges[i].val < edges[j].val
})
uf = make([]int, m*n)
for i := range uf {
uf[i] = i
}
startId, endId := 0, m*n-1
for _, e := range edges {
union(e.a, e.b)
if isConnected(startId, endId) {
return e.val
}
}
return 0
}时间复杂度 O(mnlog(mn)),空间复杂度 O(mn)。