1483. 树节点的第 K 个祖先
1483. 树节点的第 K 个祖先 (Hard)
给你一棵树,树上有 n 个节点,按从 0 到 n-1 编号。树以父节点数组的形式给出,其中 parent[i] 是节点 i 的父节点。树的根节点是编号为 0 的节点。
树节点的第 k个祖先节点是从该节点到根节点路径上的第 k 个节点。
实现 TreeAncestor 类:
TreeAncestor(int n, int[] parent)对树和父数组中的节点数初始化对象。getKthAncestor(int node, int k)返回节点node的第k个祖先节点。如果不存在这样的祖先节点,返回-1。
示例 1:
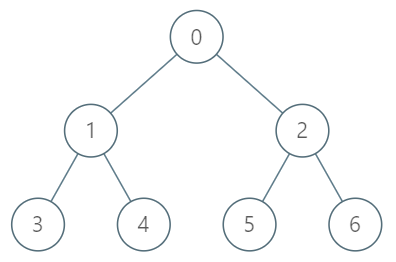
输入:
["TreeAncestor","getKthAncestor","getKthAncestor","getKthAncestor"]
[[7,[-1,0,0,1,1,2,2]],[3,1],[5,2],[6,3]]
输出:
[null,1,0,-1]
解释:
TreeAncestor treeAncestor = new TreeAncestor(7, [-1, 0, 0, 1, 1, 2, 2]);
treeAncestor.getKthAncestor(3, 1); // 返回 1 ,它是 3 的父节点
treeAncestor.getKthAncestor(5, 2); // 返回 0 ,它是 5 的祖父节点
treeAncestor.getKthAncestor(6, 3); // 返回 -1 因为不存在满足要求的祖先节点提示:
1 <= k <= n <= 5 * 10⁴parent[0] == -1表示编号为0的节点是根节点。- 对于所有的
0 < i < n,0 <= parent[i] < n总成立 0 <= node < n- 至多查询
5 * 10⁴次
分析
朴素解法仅存 parent 数组即可, 每次查询的复杂度会是 O(k)
可以用倍增的思路借助动态规划来实降低复杂度.
定义 dp[node][j] 表示节点 node 的第 2^j 个祖先, 那么可以先找到 node 的第 2^(j-1) 个祖先 x, 然后找到 x 的第 2^(j-1) 个祖先, 这就是所求, 即:
dp[node][j] = dp[dp[node][j-1]][j-1]第二个维度 k 的上限是 logn, 在这个问题约束中, n 最大为 50000, k 不会超过 16.
对于任意一个数字 k, 可以写成多个 2 的幂的和的形式, 比如 5 = (101) = (100) + (1) = 4+1, 求第 5 个祖先即先找到第一个祖先再找第一个祖先的第四个祖先.
边界情况:
dp[node][0] = parent[node]即 node 的第一个祖先即为其父节点.
type TreeAncestor struct {
dp [][]int
logn int
}
func Constructor(n int, parent []int) TreeAncestor {
logn := int(math.Log2(float64(n))) + 1
dp := make([][]int, n)
for i := range dp {
dp[i] = make([]int, logn)
for j := range dp[i] {
dp[i][j] = -1
}
dp[i][0] = parent[i]
}
for j := 1; j < logn; j++ {
for i := 0; i < n; i++ {
if dp[i][j-1] != -1 {
dp[i][j] = dp[dp[i][j-1]][j-1]
}
}
}
return TreeAncestor{
logn: logn,
dp: dp,
}
}
func (ta *TreeAncestor) GetKthAncestor(node int, k int) int {
for i := 0; i < ta.logn; i++ {
if k&(1<<i) != 0 {
node = ta.dp[node][i]
}
if node == -1 {
return -1
}
}
return node
}
/**
* Your TreeAncestor object will be instantiated and called as such:
* obj := Constructor(n, parent);
* param_1 := obj.GetKthAncestor(node,k);
*/