3218. 切蛋糕的最小总开销 I

3218. 切蛋糕的最小总开销 I (Medium)

有一个 m x n 大小的矩形蛋糕，需要切成 1 x 1 的小块。

给你整数 m ， n 和两个数组：

• horizontalCut 的大小为 m - 1 ，其中 horizontalCut[i] 表示沿着水平线 i 切蛋糕的开销。
• verticalCut 的大小为 n - 1 ，其中 verticalCut[j] 表示沿着垂直线 j 切蛋糕的开销。

一次操作中，你可以选择任意不是 1 x 1 大小的矩形蛋糕并执行以下操作之一：

1. 沿着水平线 i 切开蛋糕，开销为 horizontalCut[i] 。
2. 沿着垂直线 j 切开蛋糕，开销为 verticalCut[j] 。

每次操作后，这块蛋糕都被切成两个独立的小蛋糕。

每次操作的开销都为最开始对应切割线的开销，并且不会改变。

请你返回将蛋糕全部切成 1 x 1 的蛋糕块的 最小 总开销。

示例 1：

输入： m = 3, n = 2, horizontalCut = [1,3], verticalCut = [5]

输出： 13

解释：

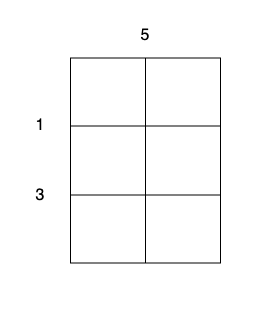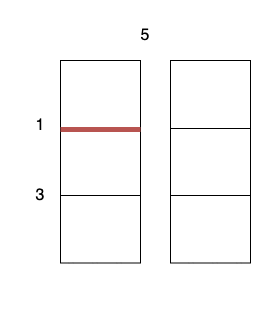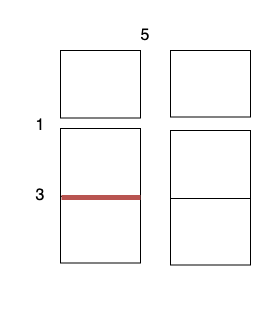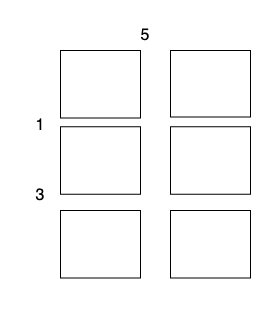
• 沿着垂直线 0 切开蛋糕，开销为 5 。
• 沿着水平线 0 切开 3 x 1 的蛋糕块，开销为 1 。
• 沿着水平线 0 切开 3 x 1 的蛋糕块，开销为 1 。
• 沿着水平线 1 切开 2 x 1 的蛋糕块，开销为 3 。
• 沿着水平线 1 切开 2 x 1 的蛋糕块，开销为 3 。

总开销为 5 + 1 + 1 + 3 + 3 = 13 。

示例 2：

输入： m = 2, n = 2, horizontalCut = [7], verticalCut = [4]

输出： 15

解释：

• 沿着水平线 0 切开蛋糕，开销为 7 。
• 沿着垂直线 0 切开 1 x 2 的蛋糕块，开销为 4 。
• 沿着垂直线 0 切开 1 x 2 的蛋糕块，开销为 4 。

总开销为 7 + 4 + 4 = 15 。

提示：

• 1 <= m, n <= 20
• horizontalCut.length == m - 1
• verticalCut.length == n - 1
• 1 <= horizontalCut[i], verticalCut[i] <= 10³

分析

贪心： 代价大的先切，又切割顺序无关，所以先排序

func minimumCost(m int, n int, horizontalCut []int, verticalCut []int) int {
	slices.SortFunc(horizontalCut, func(a, b int) int {
		return b - a
	})
	slices.SortFunc(verticalCut, func(a, b int) int {
		return b - a
	})
	h, v := 1, 1
	res := 0
	for len(horizontalCut) > 0 || len(verticalCut) > 0 {
		if len(verticalCut) == 0 || len(horizontalCut) > 0 && horizontalCut[0] >= verticalCut[0] {
			res += horizontalCut[0] * v
			h++
			horizontalCut = horizontalCut[1:]
		} else {
			res += verticalCut[0] * h
			v++
			verticalCut = verticalCut[1:]
		}
	}
	return res
}