柱状图中接雨水、找方块
42. 接雨水
难度困难
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。 示例 2:
输入:height = [4,2,0,3,2,5]
输出:9提示:
n == height.length0 <= n <= 3 * 1040 <= height[i] <= 105
分析
考虑每个位置能接到的雨水量
遍历数组,对于位置 i,考虑可以接到多少雨水。
显然这由左右两侧比当前位置高的柱子的高度来决定,实际生要找到左右两侧最高的柱子。如果知道左侧最高的高度 leftMax 和右侧最高的高度 rightMax,那么 i 处能接到雨水量为 min(leftMax, rightMax)-height[i]。
注意,可能左右侧最高的柱子也没有当前柱子 height[i] 高,接到雨水量为 0。这样的话可以让 leftMax 或 rightMax 等于 height[i],不影响结果。
为了降低复杂度,可以事先用动态规划的方式计算出前缀最大值和后缀最大值数组,再遍历一遍得到结果,这样会使线性复杂度。
func trap(height []int) int {
n := len(height)
if n == 0 {
return 0
}
prefixMax := make([]int, n)
prefixMax[0] = height[0]
for i := 1; i < n; i++ {
prefixMax[i] = max(prefixMax[i-1], height[i])
}
suffixMax := make([]int, n)
suffixMax[n-1] = height[n-1]
for i := n - 2; i >= 0; i-- {
suffixMax[i] = max(suffixMax[i+1], height[i])
}
res := 0
for i, h := range height {
res += min(prefixMax[i], suffixMax[i]) - h
}
return res
}时空复杂度都是O(n),其中 n 是数组长度。
双指针优化
实际上上边的两个数组可以用两个变量代替,这样就能降低空间复杂度。
使用左右双指针left、right 向中间凑,用两个变量 leftPeek,rightPeek 来维护左右峰值。
每次移动指针后,先根据左右指针处的值leftVal 和 rightVal 更新 leftPeek 和 rightPeek,再分情况讨论:
如果 leftVal < rightVal, 必有 leftPeek < rightPeek,可以确定 left 处的接雨水量为 leftPeek - leftVal;反之,可以确定 right 处的接雨水量为 rightPeek - rightVal。
如果确定了 left 处的结果,就向右移动 left 指针,反之向左移动 right 指针,直到两个指针相遇。
func trap(height []int) int {
n := len(height)
if n < 3 {
return 0
}
left, right := 0, n-1
leftPeek, rightPeek := 0, 0
res := 0
for left < right {
leftVal, rightVal := height[left], height[right]
leftPeek = max(leftPeek, leftVal)
rightPeek = max(rightPeek, rightVal)
if leftVal < rightVal { // 处理左侧
res += leftPeek - leftVal
left++
} else { // 处理右侧
res += rightPeek - rightVal
right--
}
}
return res
}时间复杂度 O(n),空间复杂度 O(1)。
单调栈
这个思路不容易想到。
遍历数组时维护一个单调递减栈,记录可能存水的条形块的索引。
每次如果当前柱子 i 大于栈顶索引对应的柱子,可以确定栈顶的柱子比当前 i 处柱子和栈的前一个柱子低,因此可以弹出栈顶元素并且累加答案。
如果当前柱子 i 小于或等于栈顶索引对应的条形块,将 i 入栈,意思是当前柱子被栈中的前一个条形块界定。
func trap1(height []int) int {
n := len(height)
if n < 3 {
return 0
}
res := 0
var stack []int // 记录可能存水的柱子索引
for i, v := range height {
for len(stack) > 0 && v > height[stack[len(stack)-1]] {
top := stack[len(stack)-1]
stack = stack[:len(stack)-1]
if len(stack) == 0 {
break
}
newTop := stack[len(stack)-1]
width := i - newTop - 1
boundHeight := min(v, height[newTop]) - height[top]
res += width * boundHeight
}
stack = append(stack, i)
}
return res
}时间复杂度:O(n)。单次遍历O(n) ,每个柱子最多被访问两次(由于栈的弹入和弹出),并且弹入和弹出栈都是 O(1)的。 空间复杂度:O(n)。 栈最多在阶梯型或平坦型条形块结构中占用 O(n)的空间。
84. 柱状图中最大的矩形
难度困难
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
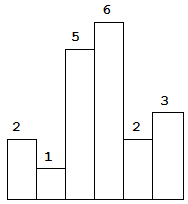
以上是柱状图的示例,其中每个柱子的宽度为 1,给定的高度为 [2,1,5,6,2,3]。
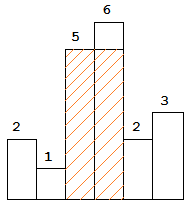
图中阴影部分为所能勾勒出的最大矩形面积,其面积为 10 个单位。
示例:
输入: [2,1,5,6,2,3]
输出: 10分析
枚举宽度
枚举所有宽度形成的矩形,如在[i,j]形成的矩形,面积 = 宽度 * heights[i:j+1] 中最小高度。
func largestRectangleArea(heights []int) int {
res := 0
for i := range heights {
for j := i; j < len(heights); j++ {
res = max(res, (j - i + 1) * min(heights[i:j+1]))
}
}
return res
}其中 min 函数计算
heights[i:j+1]中的最小值。
时间复杂度O(n^3), 空间复杂度O(1),非常不理想。
中心扩展
遍历所有高度,对每个高度向左右扩展,直到到达边界或高度小于当前高度。
func largestRectangleArea02(heights []int) int {
res := 0
for i, h := range heights {
width := 0
for left := i; left >= 1 && heights[left-1] >= h; left-- {
width++
}
for right := i; right < len(heights)-1 && heights[right+1] >= h; right++ {
width++
}
res = max(res, width*h)
}
return res
}时间复杂度 O(n^2), 空间复杂度 O(1)。
借助单调栈优化中心扩展
对于上边的中心扩展解法,可以事先借助单调递增栈来找每个位置左侧/右侧位置最近且高度小于当前位置高度的位置。
func largestRectangleArea(heights []int) int {
left, right := calLeft(heights), calRight(heights)
res := 0
for i, h := range heights {
res = max(res, (right[i]-left[i]-1)*h)
}
return res
}
// 找到每个位置左侧距离最近且高度小于当前位置高度的位置
func calLeft(heights []int) []int {
res := make([]int, len(heights))
stack := list.New()
for i, h := range heights {
for stack.Len() > 0 && heights[stack.Back().Value.(int)] >= h {
stack.Remove(stack.Back())
}
if stack.Len() == 0 {
res[i] = -1
} else {
res[i] = stack.Back().Value.(int)
}
stack.PushBack(i)
}
return res
}
// 找到每个位置右侧距离最近且高度小于当前位置的位置
func calRight(heights []int) []int {
res := make([]int, len(heights))
stack := list.New()
for i := len(heights) - 1; i >= 0; i-- {
for stack.Len() > 0 && heights[stack.Back().Value.(int)] >= heights[i] {
stack.Remove(stack.Back())
}
if stack.Len() == 0 {
res[i] = len(heights)
} else {
res[i] = stack.Back().Value.(int)
}
stack.PushBack(i)
}
return res
}时空复杂度都是 O(n)。