1489. 找到最小生成树里的关键边和伪关键边
1489. 找到最小生成树里的关键边和伪关键边
难度困难
给你一个 n 个点的带权无向连通图,节点编号为 0 到 n-1 ,同时还有一个数组 edges ,其中 edges[i] = [fromi, toi, weighti] 表示在 fromi 和 toi 节点之间有一条带权无向边。最小生成树 (MST) 是给定图中边的一个子集,它连接了所有节点且没有环,而且这些边的权值和最小。
请你找到给定图中最小生成树的所有关键边和伪关键边。如果从图中删去某条边,会导致最小生成树的权值和增加,那么我们就说它是一条关键边。伪关键边则是可能会出现在某些最小生成树中但不会出现在所有最小生成树中的边。
请注意,你可以分别以任意顺序返回关键边的下标和伪关键边的下标。
示例 1:
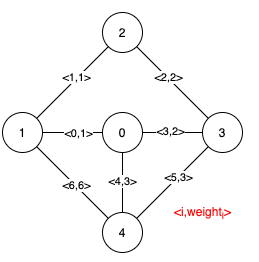
输入:n = 5, edges = [[0,1,1],[1,2,1],[2,3,2],[0,3,2],[0,4,3],[3,4,3],[1,4,6]]
输出:[[0,1],[2,3,4,5]]
解释:上图描述了给定图。
下图是所有的最小生成树。
注意到第 0 条边和第 1 条边出现在了所有最小生成树中,所以它们是关键边,我们将这两个下标作为输出的第一个列表。
边 2,3,4 和 5 是所有 MST 的剩余边,所以它们是伪关键边。我们将它们作为输出的第二个列表。示例 2 :
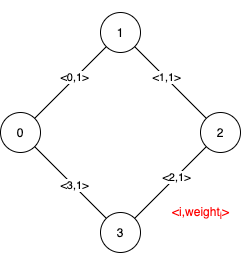
输入:n = 4, edges = [[0,1,1],[1,2,1],[2,3,1],[0,3,1]]
输出:[[],[0,1,2,3]]
解释:可以观察到 4 条边都有相同的权值,任选它们中的 3 条可以形成一棵 MST 。所以 4 条边都是伪关键边。提示:
2 <= n <= 1001 <= edges.length <= min(200, n * (n - 1) / 2)edges[i].length == 30 <= fromi < toi < n1 <= weighti <= 1000- 所有
(fromi, toi)数对都是互不相同的。
函数签名:
func findCriticalAndPseudoCriticalEdges(n int, edges [][]int) [][]int分析
如果每条边的权值都不相同,那么最小生成树就是唯一的。但因为不同边的权值有可能相同,所以最小生成树也可能有多个,比如这个问题举的几个例子。
这个问题开始探讨怎么穷举所有最小生成树。
用 Kruskal 算法,先计算出所有边参与的最小生成树的权值和 target,这里不关心是什么样的一棵树,只关心其权值和。
然后再枚举每条边:
首先判断当前边是不是关键边:尝试忽略这条边得到最小生成树,如果忽略后图无法联通或者最小生成树的权值和比 target 大,可以确定,这是一条关键边。
其次,首先把这条边加入结果生成树里,再一一添加其他的边,最后得到最小生成树。如果最终的权值和等于 target, 那么这条边是关键边或伪关键边,但因为上边已经判断多是否关键边。所以这里肯定是伪关键边。
type Edge struct {
id, u, v, val int
}
func findCriticalAndPseudoCriticalEdges(n int, edges [][]int) [][]int {
// 需要记录原始索引,即边的编号
es := make([]Edge, len(edges))
for i, e := range edges {
es[i] = Edge{id: i, u: e[0], v: e[1], val: e[2]}
}
sort.Slice(es, func(i, j int) bool {
return es[i].val < es[j].val
})
target, ok := calVal(es, NewUnionFind(n), -1)
if !ok {
return nil
}
keyEdges := make([]int, 0, len(es))
others := make([]int, 0, len(es))
for i, e := range es {
val, ok := calVal(es, NewUnionFind(n), i)
// 是否关键边
if !ok || val > target {
keyEdges = append(keyEdges, e.id)
continue
}
// 是否伪关键边
uf := NewUnionFind(n)
uf.Union(e.u, e.v)
val, _ = calVal(es, uf, i)
if e.val+val == target {
others = append(others, e.id)
}
}
return [][]int{keyEdges, others}
}
// 返回忽略边 ignore 后得到的最小生成树的总权值,如果无法联通,返回 false
func calVal(edges []Edge, uf *UnionFind, ignore int) (int, bool) {
res := 0
for i, e := range edges {
if i == ignore {
continue
}
if uf.Union(e.u, e.v) {
res += e.val
}
}
return res, uf.setCnt == 1
}
type UnionFind struct {
parent []int
setCnt int // 当前连通分量数目
}
func NewUnionFind(n int) *UnionFind {
p := make([]int, n)
for i := range p {
p[i] = i
}
return &UnionFind{parent: p, setCnt: n}
}
func (uf *UnionFind) Union(x, y int) bool {
x, y = uf.Find(x), uf.Find(y)
if x == y {
return false
}
uf.parent[x] = y
uf.setCnt--
return true
}
func (uf *UnionFind) Find(x int) int {
for x != uf.parent[x] {
x, uf.parent[x] = uf.parent[x], uf.parent[uf.parent[x]]
}
return x
}时间复杂度 O(m^2*α(n)), m 是边的总数,n 是点的总数。 空间复杂度 O(m+n)。