1334. 阈值距离内邻居最少的城市
1334. 阈值距离内邻居最少的城市 (Medium)
有 n 个城市,按从 0 到 n-1 编号。给你一个边数组 edges,其中 edges[i] = [fromᵢ, toᵢ, weightᵢ] 代表 fromᵢ 和 toᵢ 两个城市之间的双向加权边,距离阈值是一个整数 distanceThreshold。
返回能通过某些路径到达其他城市数目最少、且路径距离 最大 为 distanceThreshold 的城市。如果有多个这样的城市,则返回编号最大的城市。
注意,连接城市 i 和 j 的路径的距离等于沿该路径的所有边的权重之和。
示例 1:
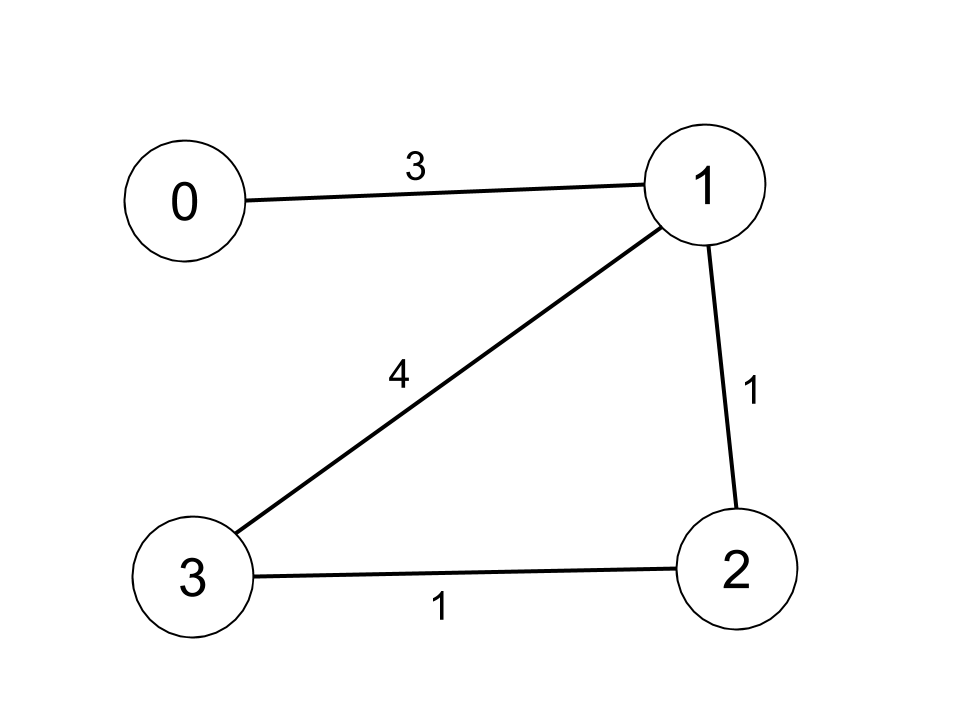
输入:n = 4, edges = [[0,1,3],[1,2,1],[1,3,4],[2,3,1]], distanceThreshold = 4
输出:3
解释:城市分布图如上。
每个城市阈值距离 distanceThreshold = 4 内的邻居城市分别是:
城市 0 -> [城市 1, 城市 2]
城市 1 -> [城市 0, 城市 2, 城市 3]
城市 2 -> [城市 0, 城市 1, 城市 3]
城市 3 -> [城市 1, 城市 2]
城市 0 和 3 在阈值距离 4 以内都有 2 个邻居城市,但是我们必须返回城市 3,因为它的编号最大。示例 2:
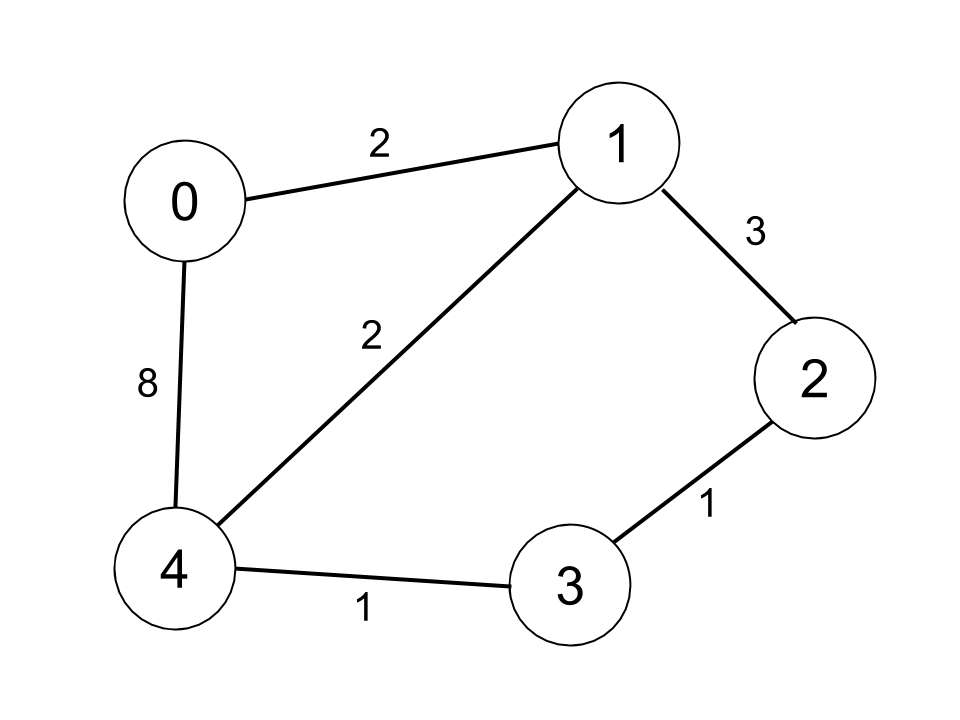
输入:n = 5, edges = [[0,1,2],[0,4,8],[1,2,3],[1,4,2],[2,3,1],[3,4,1]], distanceThreshold = 2
输出:0
解释:城市分布图如上。
每个城市阈值距离 distanceThreshold = 2 内的邻居城市分别是:
城市 0 -> [城市 1]
城市 1 -> [城市 0, 城市 4]
城市 2 -> [城市 3, 城市 4]
城市 3 -> [城市 2, 城市 4]
城市 4 -> [城市 1, 城市 2, 城市 3]
城市 0 在阈值距离 2 以内只有 1 个邻居城市。提示:
2 <= n <= 1001 <= edges.length <= n * (n - 1) / 2edges[i].length == 30 <= fromᵢ < toᵢ < n1 <= weightᵢ, distanceThreshold <= 10^4- 所有
(fromᵢ, toᵢ)都是不同的。
分析
这个问题用 bfs 或 dfs 都不容易解决,这是个典型的 Floyd 算法问题,该算法基于动态规划,时间复杂的O(n^3)。
可参考 《399. 除法求值》的解答,399 中用了 bfs、dfs、floyed 及并查集多种解法。
func findTheCity(n int, edges [][]int, distanceThreshold int) int {
const inf = math.MaxInt32
dis := make([][]int, n)
for i := range dis {
dis[i] = make([]int, n)
for j := range dis[i] {
dis[i][j] = inf
}
}
for _, e := range edges {
i, j := e[0], e[1]
dis[i][j] = e[2]
dis[j][i] = e[2]
}
for mid := 0; mid < n; mid++ {
for from := 0; from < n; from++ {
if from == mid || dis[from][mid] == inf {
continue
}
for to := from + 1; to < n; to++ {
if to == mid || dis[mid][to] == inf {
continue
}
dis[from][to] = min(dis[from][to], dis[from][mid]+dis[mid][to])
dis[to][from] = dis[from][to]
}
}
}
res := -1
cnt := inf
for i := 0; i < n; i++ {
sum := 0
for j := 0; j < n; j++ {
if i != j && dis[i][j] <= distanceThreshold {
sum++
}
}
if sum <= cnt {
cnt = sum
res = i
}
}
return res
}