1970. 你能穿过矩阵的最后一天
1970. 你能穿过矩阵的最后一天 (Hard)
给你一个下标从 1 开始的二进制矩阵,其中 0 表示陆地, 1 表示水域。同时给你 row 和 col 分别表示矩阵中行和列的数目。
一开始在第 0 天, 整个 矩阵都是 陆地 。但每一天都会有一块新陆地被 水 淹没变成水域。给你一个下标从 1 开始的二维数组 cells ,其中 cells[i] = [rᵢ, cᵢ] 表示在第 i 天,第 rᵢ 行 cᵢ 列(下标都是从 1 开始)的陆地会变成 水域 (也就是 0 变成 1 )。
你想知道从矩阵最 上面 一行走到最 下面 一行,且只经过陆地格子的 最后一天 是哪一天。你可以从最上面一行的 任意 格子出发,到达最下面一行的 任意 格子。你只能沿着 四个 基本方向移动(也就是上下左右)。
请返回只经过陆地格子能从最 上面 一行走到最 下面 一行的 最后一天 。
示例 1:
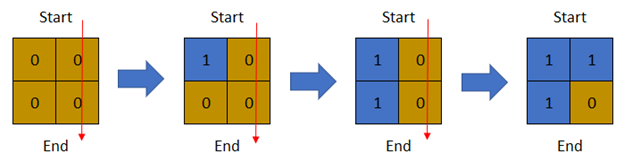
输入:row = 2, col = 2, cells = [[1,1],[2,1],[1,2],[2,2]]
输出:2
解释:上图描述了矩阵从第 0 天开始是如何变化的。
可以从最上面一行到最下面一行的最后一天是第 2 天。示例 2:
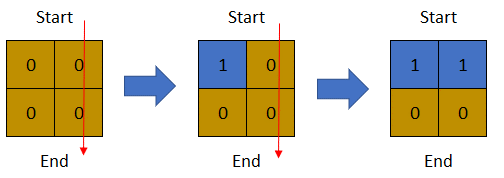
输入:row = 2, col = 2, cells = [[1,1],[1,2],[2,1],[2,2]]
输出:1
解释:上图描述了矩阵从第 0 天开始是如何变化的。
可以从最上面一行到最下面一行的最后一天是第 1 天。示例 3:
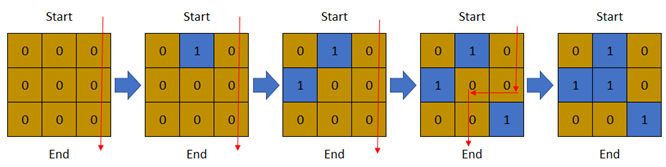
输入:row = 3, col = 3, cells = [[1,2],[2,1],[3,3],[2,2],[1,1],[1,3],[2,3],[3,2],[3,1]]
输出:3
解释:上图描述了矩阵从第 0 天开始是如何变化的。
可以从最上面一行到最下面一行的最后一天是第 3 天。提示:
2 <= row, col <= 2 * 10⁴4 <= row * col <= 2 * 10⁴cells.length == row * col1 <= rᵢ <= row1 <= cᵢ <= colcells中的所有格子坐标都是 唯一 的。
分析
没有较好的贪心策略,必须用一个 row*col 的数组来模拟。
二分
最朴素的做法:遍历 cells,每次将对应的位置置为 1,然后用 BFS 或 DFS 来检查第一行和最后一行是否联通。
有单调性,可以改进成二分 + BFS/DFS,这样时间复杂度为 O(SlogS),其中 S == row*col 即格子总数, 空间复杂度相同。
代码略。
并查集
遍历 cells,只需要判断当前情况下第一列和最后一列是否联通,这可以用并查集, 注意添加两个虚拟节点。
并查集各种操作的复杂度可以看做常数级,总体复杂度为 O(S),空间复杂度同样为 O(S)。
func latestDayToCross(row int, col int, cells [][]int) int {
grid := make([][]int, row)
for i := range grid {
grid[i] = make([]int, col)
}
total := row * col
initUF(total + 2)
left := total
right := total + 1
getID := func(r, c int) int {
return r*col + c
}
for r := 0; r < row; r++ {
id := getID(r, 0)
union(id, left)
id = getID(r, col-1)
union(id, right)
}
for i, cell := range cells {
r, c := cell[0]-1, cell[1]-1
grid[r][c] = 1
// 联通8个方向上的相邻1
for dr := -1; dr <= 1; dr++ {
for dc := -1; dc <= 1; dc++ {
if dr == 0 && dc == 0 {
continue
}
nr, nc := r+dr, c+dc
if nr < 0 || nr >= row || nc < 0 || nc >= col || grid[nr][nc] == 0 {
continue
}
union(getID(r, c), getID(nr, nc))
if find(left) == find(right) {
return i
}
}
}
}
return len(cells)
}
var uf []int
func initUF(n int) {
uf = make([]int, n)
for i := range uf {
uf[i] = i
}
}
func find(x int) int {
for x != uf[x] {
x, uf[x] = uf[x], uf[uf[x]]
}
return x
}
func union(x, y int) {
x, y = find(x), find(y)
uf[x] = y
}测试用例:
func Test_latestDayToCross(t *testing.T) {
type args struct {
row int
col int
cells [][]int
}
tests := []struct {
name string
args args
want int
}{
{args: args{6, 2, [][]int{{2, 1}, {4, 2}, {6, 2}, {4, 1}, {1, 2}}}, want: 3},
}
for _, tt := range tests {
if got := latestDayToCross(tt.args.row, tt.args.col, tt.args.cells); got != tt.want {
t.Errorf("%q. latestDayToCross() = %v, want %v", tt.name, got, tt.want)
}
}
}逆向并查集
如果不考虑最左最右两列的连通性,而是考虑最上最下两行的连通性,需要逆向思考,参考:打砖块,代码略。