1579. 保证图可完全遍历
1579. 保证图可完全遍历
难度困难
Alice 和 Bob 共有一个无向图,其中包含 n 个节点和 3 种类型的边:
- 类型 1:只能由 Alice 遍历。
- 类型 2:只能由 Bob 遍历。
- 类型 3:Alice 和 Bob 都可以遍历。
给你一个数组 edges ,其中 edges[i] = [typei, ui, vi] 表示节点 ui 和 vi 之间存在类型为 typei 的双向边。请你在保证图仍能够被 Alice和 Bob 完全遍历的前提下,找出可以删除的最大边数。如果从任何节点开始,Alice 和 Bob 都可以到达所有其他节点,则认为图是可以完全遍历的。
返回可以删除的最大边数,如果 Alice 和 Bob 无法完全遍历图,则返回 -1 。
示例 1:
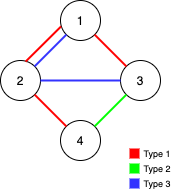
输入:n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]
输出:2
解释:如果删除 [1,1,2] 和 [1,1,3] 这两条边,Alice 和 Bob 仍然可以完全遍历这个图。再删除任何其他的边都无法保证图可以完全遍历。所以可以删除的最大边数是 2 。示例 2:
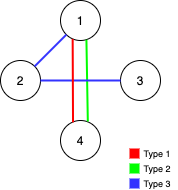
输入:n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]]
输出:0
解释:注意,删除任何一条边都会使 Alice 和 Bob 无法完全遍历这个图。示例 3:
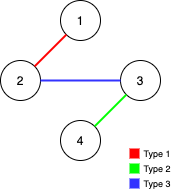
输入:n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]]
输出:-1
解释:在当前图中,Alice 无法从其他节点到达节点 4 。类似地,Bob 也不能达到节点 1 。因此,图无法完全遍历。提示:
1 <= n <= 10^51 <= edges.length <= min(10^5, 3 * n * (n-1) / 2)edges[i].length == 31 <= edges[i][0] <= 31 <= edges[i][1] < edges[i][2] <= n- 所有元组
(typei, ui, vi)互不相同
函数签名:
func maxNumEdgesToRemove(n int, edges [][]int) int分析
尝试借助并查集解决。一开始将所有 n 个点看作各自为政的散点,根据 edges 来连接这些点。
按照题目诉求,要尽可能地少用边。首先可以确定,优先用类型为 3 即 Alice 和 Bob 都能通过的边较好。
先尽可能用 Alice 和 Bob 的共用边是对的:对于两个联通分量,如果要联通它们,可以用一条共用类型的边或者两条独用类型的边,显然用共用类型的边将省一条边。
为 Alice 和 Bob 分别创建一个并查集。先根据所有类型为 3 的边,对这两个并查集分别做一一合并,之后再分别针对独用边,对两个并查集做一一合并。
注意如果两个点已经联通则无需再合并,对应的边应该舍弃。
type UnionFind struct {
parent []int
set int
}
func NewUnionFind(n int) *UnionFind {
p := make([]int, n)
for i := range p {
p[i] = i
}
return &UnionFind{parent: p, set: n}
}
func (uf *UnionFind) Find(x int) int {
for x != uf.parent[x] {
x, uf.parent[x] = uf.parent[x], uf.parent[uf.parent[x]]
}
return uf.parent[x]
}
func (uf *UnionFind) Union(x, y int) bool {
x, y = uf.Find(x), uf.Find(y)
if x == y {
return false
}
uf.parent[x] = y
uf.set--
return true
}
func maxNumEdgesToRemove(n int, edges [][]int) int {
if n-1 > len(edges) {
return -1
}
alice, bob := NewUnionFind(n), NewUnionFind(n)
res := 0
for _, e := range edges {
if e[0] != 3 {
continue
}
if alice.Union(e[1]-1, e[2]-1) {
bob.Union(e[1]-1, e[2]-1)
} else {
res++
}
}
for _, e := range edges {
if e[0] == 1 && !alice.Union(e[1]-1, e[2]-1) ||
e[0] == 2 && !bob.Union(e[1]-1, e[2]-1) {
res++
}
}
if alice.set != 1 || bob.set != 1 {
return -1
}
return res
}