1203. 项目管理
1203. 项目管理
难度困难
公司共有 n 个项目和 m 个小组,每个项目要不无人接手,要不就由 m 个小组之一负责。
group[i] 表示第 i 个项目所属的小组,如果这个项目目前无人接手,那么 group[i] 就等于 -1。(项目和小组都是从零开始编号的)小组可能存在没有接手任何项目的情况。
请你帮忙按要求安排这些项目的进度,并返回排序后的项目列表:
- 同一小组的项目,排序后在列表中彼此相邻。
- 项目之间存在一定的依赖关系,我们用一个列表
beforeItems来表示,其中beforeItems[i]表示在进行第i个项目前(位于第i个项目左侧)应该完成的所有项目。
如果存在多个解决方案,只需要返回其中任意一个即可。如果没有合适的解决方案,就请返回一个 空列表 。
示例 1:
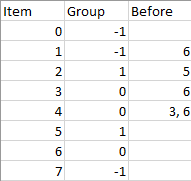
输入:n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]]
输出:[6,3,4,1,5,2,0,7]示例 2:
输入:n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3],[],[4],[]]
输出:[]
解释:与示例 1 大致相同,但是在排序后的列表中,4 必须放在 6 的前面。提示:
1 <= m <= n <= 3 * 104group.length == beforeItems.length == n-1 <= group[i] <= m - 10 <= beforeItems[i].length <= n - 10 <= beforeItems[i][j] <= n - 1i != beforeItems[i][j]beforeItems[i]不含重复元素
函数签名:
func sortItems(n int, m int, group []int, beforeItems [][]int) []int分析
比较复杂的拓扑排序,可以先看看简单点的拓扑排序问题:课程表。
花了两天研究这个问题,经历了四个阶段:
官方题解两重 bfs 拓扑排序 -> 尝试两重 dfs 拓扑排序 ->
发现一重 dfs 拓扑排序解法 -> 写出一重 bfs 拓扑排序解法终于完全搞明白了这个问题,收益良多。
两重拓扑排序
因为不同的项目有先后顺序,又分配给了不同的小组,这样导致最终小组要有拓扑序,每个小组内部的项目也要有拓扑序。
范围需要从大到小,先处理各个小组的顺序,再处理每个小组内部的项目顺序。处理过程都是拓扑排序。
这样就需要事先对没有分配小组的项目做特殊处理,让它们归属于某个虚拟的小组。
func sortItems(n int, m int, group []int, beforeItems [][]int) []int {
/*
为了后续计算方便,先统计每个小组分到的项目
对于没有分到小组的项目 i ,分派给虚拟组 m + i;容易看到,一个虚拟组只会分到一个项目
极端情况所有的 n 个项目都没有分配给具体小组,这样虚拟小组就有 n 个,总的小组数目是 m+n
这样需要假设总共有 m+n 个小组,空间可能并没有被完全利用,但是这不影响结果
*/
teamItems := make([][]int, m+n)
for item, team := range group {
if team == -1 { // 没有安排小组的项目安排给一个虚拟小组
team = m + item
group[item] = team
}
teamItems[team] = append(teamItems[team], item)
}
beforeTeams := make([][]int, m+n) // 记录小组间先后关系
for curItem, preItems := range beforeItems {
curTeam := group[curItem]
for _, preItem := range preItems {
preTeam := group[preItem]
if curTeam != preTeam { // 两个项目安排给了不同的小组, 因 curItem 依赖 preItem,所以 curTeam 依赖 preTeam
beforeTeams[curTeam] = append(beforeTeams[curTeam], preTeam)
}
}
}
sortedTeams := getSortedTeams(m+n, beforeTeams)
if sortedTeams == nil {
return nil
}
res := make([]int, 0, n)
flags := make([]int, n)
for _, team := range sortedTeams {
items := teamItems[team]
sortedItems := topSort(beforeItems, items, flags)
if sortedItems == nil {
return nil
}
res = append(res, sortedItems...)
}
return res
}
func getSortedTeams(n int, dependency [][]int) []int {
teams := make([]int, n)
for i := range teams {
teams[i] = i
}
return topSort(dependency, teams, make([]int, n))
}
// 拓扑排序,将 items 按照拓扑序排列
func topSort(dependency [][]int, items, flags []int) []int {
res := make([]int, 0, len(flags))
var dfs func(int) bool
dfs = func(cur int) bool {
if flags[cur] == 1 {
return true
}
if flags[cur] == -1 {
return false
}
flags[cur] = -1
for _, next := range dependency[cur] {
if !dfs(next) {
return false
}
}
flags[cur] = 1
res = append(res, cur)
return true
}
for _, v := range items {
if !dfs(v) {
return nil
}
}
return res
}上边是用 dfs 的方式求拓扑序,在最后一个用例超时了。改用 bfs 的方式:
func sortItems(n int, m int, group []int, beforeItems [][]int) []int {
teamItems := make([][]int, m+n)
for item, team := range group {
if team == -1 { // 没有安排小组的项目安排给一个虚拟小组
team = m + item
group[item] = team
}
teamItems[team] = append(teamItems[team], item)
}
teamGraph := make([][]int, m+n) // 记录小组间先后关系
teamDegree := make([]int, m+n)
itemGraph := make([][]int, n) // 记录项目间先后关系
itemDegree := make([]int, n)
for curItem, preItems := range beforeItems {
curTeam := group[curItem]
for _, preItem := range preItems {
preTeam := group[preItem]
if curTeam == preTeam { // 两个项目安排给了同一个小组
itemDegree[curItem]++
itemGraph[preItem] = append(itemGraph[preItem], curItem)
} else { // 两个项目安排给了不同的小组
teamDegree[curTeam]++
teamGraph[preTeam] = append(teamGraph[preTeam], curTeam)
}
}
}
sortedTeams := getSortedTeams(m+n, teamGraph, teamDegree)
if len(sortedTeams) < m+n {
return nil
}
res := make([]int, 0, n)
for _, team := range sortedTeams {
items := teamItems[team]
sortedItems := topSort(itemGraph, itemDegree, items)
if len(sortedItems) < len(items) {
return nil
}
res = append(res, sortedItems...)
}
return res
}
func getSortedTeams(n int, teamGraph [][]int, teamDegree []int) []int {
teams := make([]int, n)
for i := range teams {
teams[i] = i
}
return topSort(teamGraph, teamDegree, teams)
}
// 拓扑排序,将 items 按照拓扑序排列
func topSort(nexts [][]int, degree []int, items []int) []int {
res := make([]int, 0, len(items))
queue := list.New()
for _, v := range items {
if degree[v] == 0 {
queue.PushBack(v)
}
}
for queue.Len() > 0 {
cur := queue.Remove(queue.Front()).(int)
res = append(res, cur)
for _, next := range nexts[cur] {
degree[next]--
if degree[next] == 0 {
queue.PushBack(next)
}
}
}
return res
}时间复杂度和空间复杂度都是 O(n+m), 其中 n 和 m 分别代表顶点和边的数量。
一重拓扑排序
上面的实现有两重拓扑排序,还可以转化成一重。
这里有个转化思路 。
通过给每个小组增加两个节点,起始点和结束点,对于一个特定的小组,对其他组的依赖关系可以表示为该组的起点对其他组的终点的依赖,这样将拓扑排序降为一重了。最后删除多添加的起点和终点即可。
dfs 做拓扑排序的时候要注意 先对额外添加的节点做 dfs, bfs 排序的时候注意用栈而不是队列,这两个细节保证了同一个组的项目会连续排列在一起。详见如下代码及分析:
func sortItems(n int, m int, group []int, beforeItems [][]int) []int {
dependency := wrap(n, m, group, beforeItems)
res := topSort(dependency)
return filter(res, n)
}
func wrap(n int, m int, group []int, beforeItems [][]int) [][]int {
dependency := make([][]int, n+2*m)
for item := 0; item < n; item++ {
curTeam := group[item]
if curTeam != -1 {
// n+curTeam 作为 curTeam 小组的起点 ,组内其他点依赖该点,当前为 item 依赖该点
dependency[item] = append(dependency[item], n+curTeam)
// n+m+curTeam 作为 curTeam 小组的终点 ,该点依赖组内其他点,当前依赖的是 item 点
dependency[n+m+curTeam] = append(dependency[n+m+curTeam], item)
}
for _, preItem := range beforeItems[item] {
preTeam := group[preItem]
if curTeam != -1 && curTeam == preTeam {
dependency[item] = append(dependency[item], preItem)
continue
}
// i, j 分别为当前组的起点和前一个组的终点
i, j := item, preItem
if curTeam != -1 {
i = n + curTeam
}
if preTeam != -1 {
j = n + m + preTeam
}
dependency[i] = append(dependency[i], j)
}
}
return dependency
}
func topSort(dependency [][]int) []int {
n := len(dependency)
res := make([]int, 0, n)
flags := make([]int, n)
var dfs func(int) bool
dfs = func(cur int) bool {
if flags[cur] != 0 {
return flags[cur] == 1
}
flags[cur] = -1
for _, pre := range dependency[cur] {
if !dfs(pre) {
return false
}
}
flags[cur] = 1
res = append(res, cur)
return true
}
// 注意是倒序,先用额外添加的大于等于 n 的节点排序,保证组与组的顺序
for i := n - 1; i >= 0; i-- {
if !dfs(i) {
return nil
}
}
return res
}// 剔除 s 中额外添加的节点
func filter(s []int, n int) []int {
res := make([]int, 0, n)
for _, v := range s {
if v < n {
res = append(res, v)
}
}
return res
}上边是 dfs 的写法,以下是 bfs 的写法,
不同于一般的 bfs 不要求节点出集合(一般用一个队列)的顺序,这里为了保证同一个组的节点连续在一起出集合,集合用栈:
func sortItems(n int, m int, group []int, beforeItems [][]int) []int {
nexts, degree := wrap(n, m, group, beforeItems)
res := topSort(nexts, degree)
return filter(res, n)
}
func wrap(n int, m int, group []int, beforeItems [][]int) ([][]int, []int) {
nexts := make([][]int, n+2*m)
degree := make([]int, n+2*m)
for item := 0; item < n; item++ {
curTeam := group[item]
if curTeam != -1 {
// n+curTeam 作为 curTeam 小组的起点 ,组内其他点依赖该点,当前为 item 依赖该点
degree[item]++
nexts[n+curTeam] = append(nexts[n+curTeam], item)
// n+m+curTeam 作为 curTeam 小组的终点 ,该点依赖组内其他点,当前依赖的是 item 点
degree[n+m+curTeam]++
nexts[item] = append(nexts[item], n+m+curTeam)
}
for _, preItem := range beforeItems[item] {
preTeam := group[preItem]
if curTeam != -1 && curTeam == preTeam {
nexts[preItem] = append(nexts[preItem], item)
degree[item]++
continue
}
// i, j 分别为当前组的起点和前一个组的终点
i, j := item, preItem
if curTeam != -1 {
i = n + curTeam // curTeam 组的起点
}
if preTeam != -1 {
j = n + m + preTeam // preTeam 组的终点
}
nexts[j] = append(nexts[j], i)
degree[i]++
}
}
return nexts, degree
}
func topSort(nexts [][]int, degree []int) []int {
n := len(nexts)
res := make([]int, 0, n)
// 节点后进先出,保证同一组的节点连续输出
stack := list.New()
for i := 0; i < n; i++ {
if degree[i] == 0 {
stack.PushBack(i)
}
}
for stack.Len() > 0 {
cur := stack.Remove(stack.Back()).(int)
res = append(res, cur)
for _, next := range nexts[cur] {
degree[next]--
if degree[next] == 0 {
stack.PushBack(next)
}
}
}
if len(res) < n {
return nil
}
return res
}时间复杂度和空间复杂度都是 O(n+m), 其中 n 和 m 分别代表顶点和边的数量。
实测一重拓扑派序的 dfs 解法效率最高,其次是一重拓扑排序的 bfs 解法,其次是两重拓扑排序的 bfs 解法, 两重拓扑排序的 dfs 解法有一个用例超时。