2471. 逐层排序二叉树所需的最少操作数目
2471. 逐层排序二叉树所需的最少操作数目
难度中等
给你一个 值互不相同 的二叉树的根节点 root 。
在一步操作中,你可以选择 同一层 上任意两个节点,交换这两个节点的值。
返回每一层按 严格递增顺序 排序所需的最少操作数目。
节点的 层数 是该节点和根节点之间的路径的边数。
示例 1 :
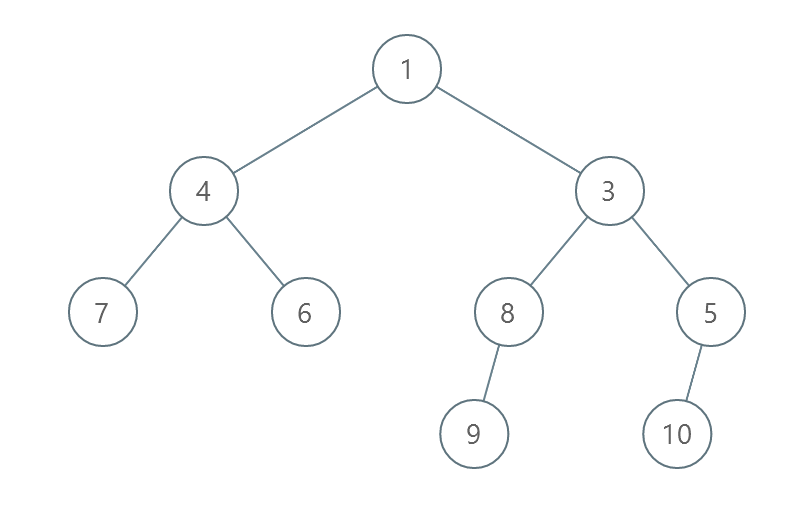
输入: root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10] 输出: 3 解释:
- 交换 4 和 3 。第 2 层变为 [3,4] 。
- 交换 7 和 5 。第 3 层变为 [5,6,8,7] 。
- 交换 8 和 7 。第 3 层变为 [5,6,7,8] 。 共计用了 3 步操作,所以返回 3 。 可以证明 3 是需要的最少操作数目。
示例 2 :
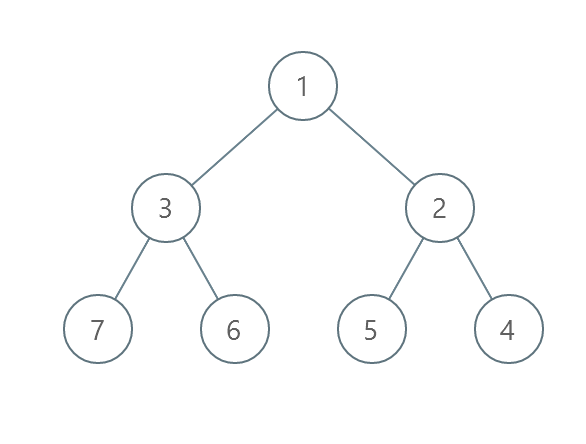
输入: root = [1,3,2,7,6,5,4] 输出: 3 解释:
- 交换 3 和 2 。第 2 层变为 [2,3] 。
- 交换 7 和 4 。第 3 层变为 [4,6,5,7] 。
- 交换 6 和 5 。第 3 层变为 [4,5,6,7] 。 共计用了 3 步操作,所以返回 3 。 可以证明 3 是需要的最少操作数目。
示例 3 :
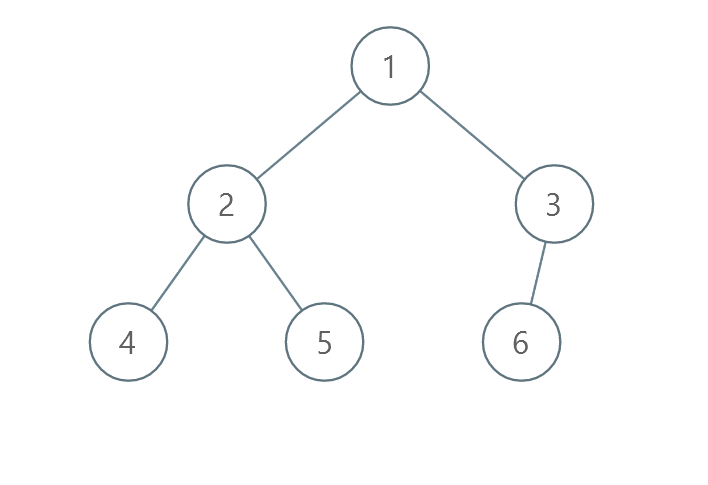
输入: root = [1,2,3,4,5,6] 输出: 0 解释: 每一层已经按递增顺序排序,所以返回 0 。
提示:
- 树中节点的数目在范围
[1, 105]。 1 <= Node.val <= 105- 树中的所有值 互不相同 。
函数签名:
func minimumOperations(root *TreeNode) int分析
显然需要用 BFS 的方式遍历每一层,对于每一层的元素,计算出使其变为有序的最小操作次数,累加这些次数即可。
难点在于怎么计算每层需要的最少操作次数,这是一个经典问题见 Minimum number of swaps required to sort an array - GeeksforGeeks。
func minimumOperations(root *TreeNode) int {
if root == nil {
return 0
}
res := 0
level := []*TreeNode{root}
for len(level) > 0 {
tmp := make([]*TreeNode, 0, 2*len(level))
for _, v := range level {
if v.Left != nil {
tmp = append(tmp, v.Left)
}
if v.Right != nil {
tmp = append(tmp, v.Right)
}
}
level = tmp
res += cal(level)
}
return res
}核心 cal 函数的实现如下:
// 可以任意交换数组元素,计算最终让数组有序需要的最少操作数
// 经典问题,见 https://www.geeksforgeeks.org/minimum-number-swaps-required-sort-array
func cal(ori []*TreeNode) int {
n := len(ori)
idx := make([]int, n)
for i := range idx {
idx[i] = i
}
sort.Slice(idx, func(i, j int) bool {
return ori[idx[i]].Val < ori[idx[j]].Val
})
// 类似并查集的思路,起初有 n 个散点,把所有成环的元素联通,最终结果就是 n - 联通分量都个数
seen := make([]bool, n)
for _, id := range idx {
if seen[id] {
continue
}
for !seen[id] { // 将同一个环里的元素标为访问过
seen[id] = true
id = idx[id]
}
n--
}
return n
}时间复杂度:O(nlogn),主要花费在排序上;空间复杂度 O(n)。其中 指二叉树节点个数。