587. 安装栅栏
587. 安装栅栏
难度困难
在一个二维的花园中，有一些用 (x, y) 坐标表示的树。由于安装费用十分昂贵，你的任务是先用最短的绳子围起所有的树。只有当所有的树都被绳子包围时，花园才能围好栅栏。你需要找到正好位于栅栏边界上的树的坐标。
示例 1:
输入: [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]]
输出: [[1,1],[2,0],[4,2],[3,3],[2,4]]
解释:
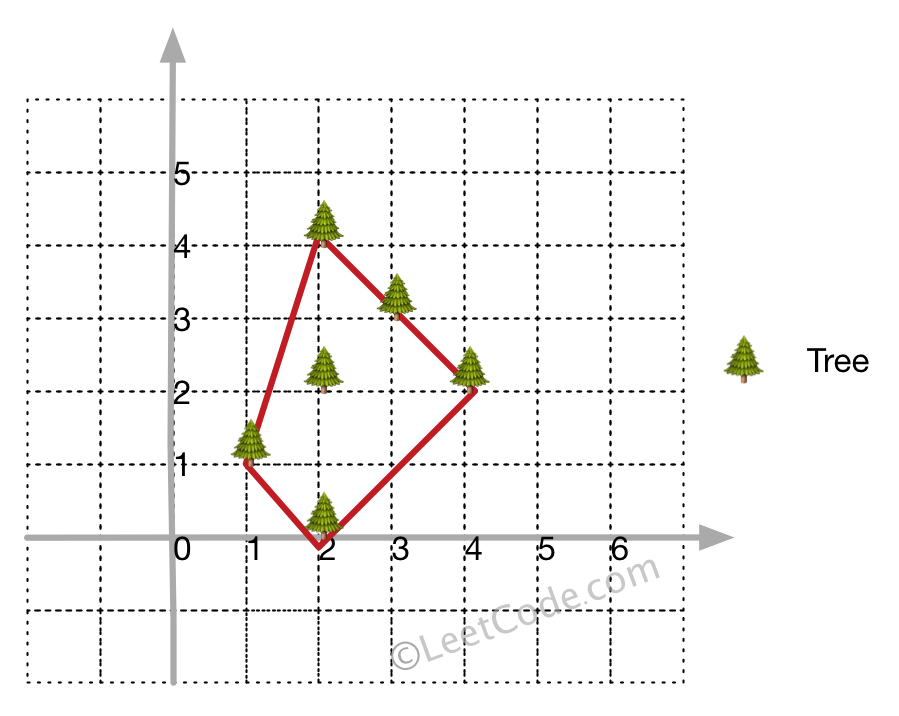
示例 2:
输入: [[1,2],[2,2],[4,2]]
输出: [[1,2],[2,2],[4,2]]
解释:
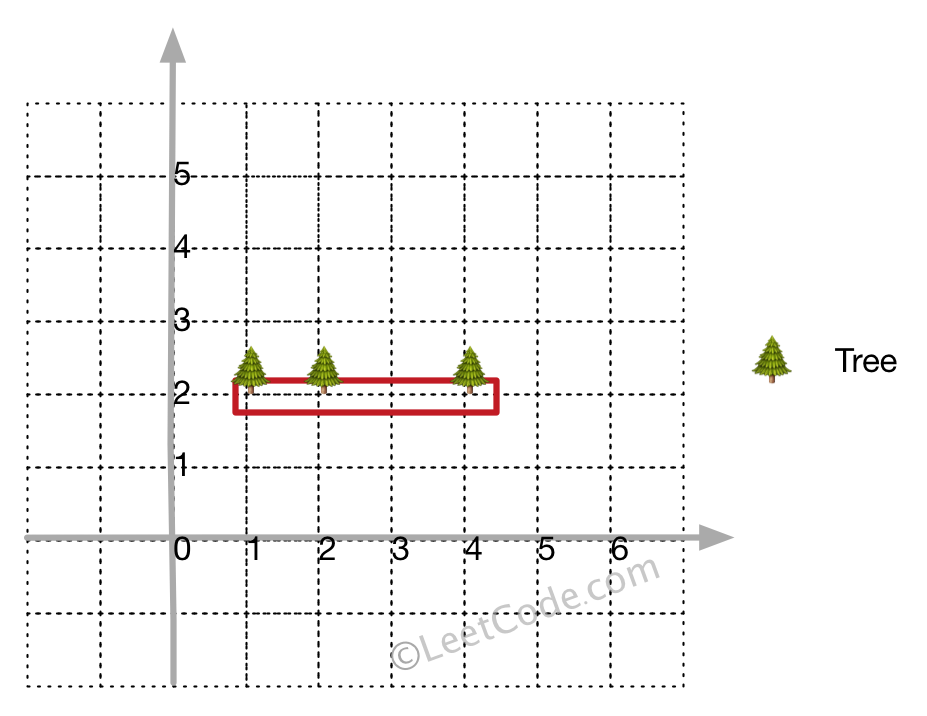即使树都在一条直线上，你也需要先用绳子包围它们。
注意:
- 所有的树应当被围在一起。你不能剪断绳子来包围树或者把树分成一组以上。
- 输入的整数在 0 到 100 之间。
- 花园至少有一棵树。
- 所有树的坐标都是不同的。
- 输入的点没有顺序。输出顺序也没有要求。
函数签名：
func outerTrees(trees [][]int) [][]int分析
可以根据坐标找到左下角的一个点，这个点一定在最外侧。
之后可以用解析几何中向量的叉乘运算，来不断找到其他外围点。
朴素解法
从左下角开始，顺时针（或逆时针）不断寻找外围的点。
func outerTrees(trees [][]int) [][]int {
n := len(trees)
if n < 4 {
return trees
}
leftBottom := getLeftBottom(trees)
p := leftBottom
vis := make([]bool, n)
res := [][]int{trees[p]}
vis[p] = true
for {
q := (p+1)%n
for r := range trees {
if r != p && r != q && cross(trees[p], trees[q], trees[r]) > 0 {
q = r
}
}
// q 点加入结果
if !vis[q] {
vis[q] = true
res = append(res, trees[q])
}
// 与pq共线的点同样加入结果
for i := range trees {
if !vis[i] && i != p && i != q && cross(trees[p], trees[q], trees[i]) == 0 {
vis[i] = true
res = append(res, trees[i])
}
}
p = q
if q == leftBottom {
break
}
}
return res
}
func getLeftBottom(points [][]int) int {
k := 0
for i, v := range points {
if v[0] < points[k][0] || v[0] == points[k][0] && v[1] < points[k][1] {
k = i
}
}
return k
}
// 向量 pq 与 qr 的叉乘
// 如果为正表示 r 点在 pq 的左侧，为负表示 r 点在 pq 的右侧，为0表示三点共线
func cross(p, q, r []int) int {
x1, y1, x2, y2 := q[0]-p[0], q[1]-p[1], r[0]-q[0], r[1]-q[1]
return x1*y2-x2*y1
}时间复杂度为O(n^2), 空间复杂度O(n)。
优化
在找到左下角的点后，可以以该点作为原点，将其他点按照极角大小排序，然后用类似单调栈的方式得到结果。这样可以把时间复杂度降到O(nlogn)。
func outerTrees(trees [][]int) [][]int {
n := len(trees)
if n < 4 {
return trees
}
p := getLeftBottom(trees)
trees[0], trees[p] = trees[p], trees[0]
tr := trees[1:]
sort.Slice(tr, func(i, j int) bool {
c := cross(trees[0], tr[i], tr[j])
if c == 0 {
return dist(trees[0], tr[i]) < dist(trees[0], tr[j])
}
return c > 0
})
// 外围最后一条边上的点按照距离从大到小排序
lo := n - 2
for lo >= 0 && cross(trees[0], trees[n-1], trees[lo]) == 0 {
lo--
}
for lo, hi := lo+1, n-1; lo < hi; lo, hi = lo+1, hi-1 {
trees[lo], trees[hi] = trees[hi], trees[lo]
}
res := [][]int{trees[0], trees[1]}
for i := 2; i < n; i++ {
for len(res) > 2 && cross(res[len(res)-2], res[len(res)-1], trees[i]) < 0 {
res = res[:len(res)-1]
}
res = append(res, trees[i])
}
return res
}
func getLeftBottom(points [][]int) int {
k := 0
for i, v := range points {
if v[0] < points[k][0] || v[0] == points[k][0] && v[1] < points[k][1] {
k = i
}
}
return k
}
// 向量 pq 与 qr 的叉乘
// 如果为正表示 r 点在 pq 的左侧，为负表示 r 点在 pq 的右侧，为0表示三点共线
func cross(p, q, r []int) int {
return (q[0]-p[0])*(r[1]-q[1]) - (q[1]-p[1])*(r[0]-q[0])
}
func dist(p, q []int) int {
return (p[0]-q[0])*(p[0]-q[0]) + (p[1]-q[1])*(p[1]-q[1])
}