1373. 二叉搜索子树的最大键值和
1373. 二叉搜索子树的最大键值和
难度困难
给你一棵以 root 为根的 二叉树 ,请你返回 任意 二叉搜索子树的最大键值和。
二叉搜索树的定义如下:
- 任意节点的左子树中的键值都 小于 此节点的键值。
- 任意节点的右子树中的键值都 大于 此节点的键值。
- 任意节点的左子树和右子树都是二叉搜索树。
示例 1:
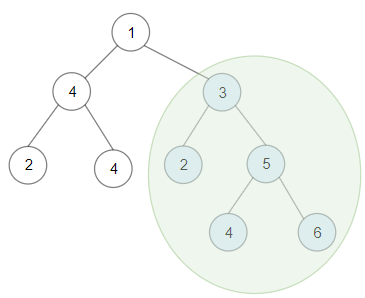
输入:root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
输出:20
解释:键值为 3 的子树是和最大的二叉搜索树。示例 2:
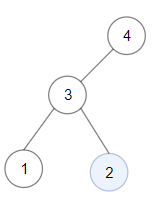
输入:root = [4,3,null,1,2]
输出:2
解释:键值为 2 的单节点子树是和最大的二叉搜索树。示例 3:
输入:root = [-4,-2,-5]
输出:0
解释:所有节点键值都为负数,和最大的二叉搜索树为空。示例 4:
输入:root = [2,1,3]
输出:6示例 5:
输入:root = [5,4,8,3,null,6,3]
输出:7提示:
- 每棵树最多有
40000个节点。 - 每个节点的键值在
[-4 * 10^4 , 4 * 10^4]之间。
函数签名:
func maxSumBST(root *TreeNode) int分析
在二叉树上做动态规划
为了得到结果,需要以某种顺序遍历每个节点。在遍历过程中,对于当前节点,需要以下信息确定是不是 BST:
左右子树是否为 BST,左子树的最大值、右子树的最小值。
最终判断当前节点为根的树是 BST 后还要计算所有节点和,这可以通过事先计算左右子树的和,之后加上自身的键值得到。
综上,需要后序遍历,每次返回以当前节点为根的子树最小值、最大值、和及是否为 BST 四个信息。
func maxSumBST(root *TreeNode) int {
var res int
var dfs func(*TreeNode) (bool, int, int, int)
dfs = func(node *TreeNode) (bool, int, int, int) {
if node == nil {
return true, math.MaxInt64, math.MinInt64, 0
}
lIsBST, lMin, lMax, lSum := dfs(node.Left)
rIsBST, rMin, rMax, rSum := dfs(node.Right)
isBST := lIsBST && rIsBST && lMax < node.Val && node.Val < rMin
sum := lSum + rSum + node.Val
if isBST {
res = max(res, sum)
}
return isBST, min(node.Val, lMin, rMin), max(node.Val, lMax, rMax), sum
}
dfs(root)
return res
}辅助函数如下:
func min(s ...int) int {
res := s[0]
for _, v := range s {
if v < res {
res = v
}
}
return res
}
func max(s ...int) int {
res := s[0]
for _, v := range s {
if v > res {
res = v
}
}
return res
}