2477. 到达首都的最少油耗

2477. 到达首都的最少油耗

难度中等

给你一棵 n 个节点的树（一个无向、连通、无环图），每个节点表示一个城市，编号从 0 到 n - 1 ，且恰好有 n - 1 条路。0 是首都。给你一个二维整数数组 roads ，其中 roads[i] = [ai, bi] ，表示城市 ai 和 bi 之间有一条 双向路 。

每个城市里有一个代表，他们都要去首都参加一个会议。

每座城市里有一辆车。给你一个整数 seats 表示每辆车里面座位的数目。

城市里的代表可以选择乘坐所在城市的车，或者乘坐其他城市的车。相邻城市之间一辆车的油耗是一升汽油。

请你返回到达首都最少需要多少升汽油。

示例 1：

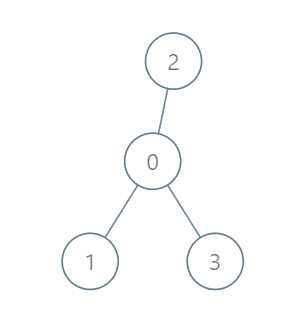
输入： roads = [[0,1],[0,2],[0,3]], seats = 5 输出： 3 解释：

• 代表 1 直接到达首都，消耗 1 升汽油。
• 代表 2 直接到达首都，消耗 1 升汽油。
• 代表 3 直接到达首都，消耗 1 升汽油。 最少消耗 3 升汽油。

示例 2：

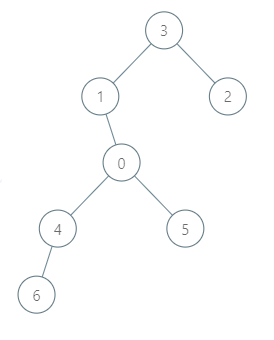
输入： roads = [[3,1],[3,2],[1,0],[0,4],[0,5],[4,6]], seats = 2 输出： 7 解释：

• 代表 2 到达城市 3 ，消耗 1 升汽油。
• 代表 2 和代表 3 一起到达城市 1 ，消耗 1 升汽油。
• 代表 2 和代表 3 一起到达首都，消耗 1 升汽油。
• 代表 1 直接到达首都，消耗 1 升汽油。
• 代表 5 直接到达首都，消耗 1 升汽油。
• 代表 6 到达城市 4 ，消耗 1 升汽油。
• 代表 4 和代表 6 一起到达首都，消耗 1 升汽油。 最少消耗 7 升汽油。

示例 3：

输入： roads = [], seats = 1 输出： 0 解释： 没有代表需要从别的城市到达首都。

提示：

• 1 <= n <= 105
• roads.length == n - 1
• roads[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• roads 表示一棵合法的树。
• 1 <= seats <= 105

分析

先考虑一种简单的情况，即每个人都自己开车而不搭车（相当于seats==1），应该怎么计算总油耗呢？

从首都开始递归，对于当前节点，总油耗就是所有子树节点个数的和。

这样可以比较容易地写出代码：

func minimumFuelCost(roads [][]int, seats int) int64 {
    n := len(roads)+1
    graph := make([][]int, n)
    for _, road := range roads {
        u, v := road[0], road[1]
        graph[u] = append(graph[u], v)
        graph[v] = append(graph[v], u)
    }

    var res int64

    var dfs func(cur, parent int) int
    dfs = func(cur, parent int) int {
        cnt := 1
        for _, v := range graph[cur] {
            if v != parent {
                cnt += dfs(v, cur)
            }
        }
        if cur != 0 { // 对于首都这个节点不要加
            res += int64(cnt)
        }
        
        return cnt
    }

    _ = dfs(0, -1)

    return res
}

现在考虑每辆车可以容纳多人即 seats > 1的情况。

总思路和上边一样，同样从首都开始递归，对于当前节点，计算出所有子树节点个数和 cnt，对于 cnt 个人，最少需要多少辆车呢？

是 (cnt+seats-1)/seats。

所以只需要把上面代码中更新 res 的那一行 res += int64(cnt) 改成 res += int64((cnt+seats-1)/seats)即可。

时间复杂度: O(n), 需要遍历所以节点；空间复杂度 O(h)， h 是递归栈的大小，即已首都为根的树的最大高度，最坏情况为 n。

扩展

如果每个城市不仅一个代表呢？如果每两个城市之间的油耗不同呢？

思路不变，只是在算总人数和总油耗的时候细节略有不同。

如果每辆车的 seats 不一样呢？—— 这个略微复杂了，需要贪心地安排车载人，优先安排容量大的车；这需要维护最优情况下到达当前节点的车的列表。时间、空间复杂度立马上来了。