1361. 验证二叉树
1361. 验证二叉树
难度中等
二叉树上有 n 个节点,按从 0 到 n - 1 编号,其中节点 i 的两个子节点分别是 leftChild[i] 和 rightChild[i]。
只有 所有 节点能够形成且 只 形成 一棵 有效的二叉树时,返回 true;否则返回 false。
如果节点 i 没有左子节点,那么 leftChild[i] 就等于 -1。右子节点也符合该规则。
注意:节点没有值,本问题中仅仅使用节点编号。
示例 1:
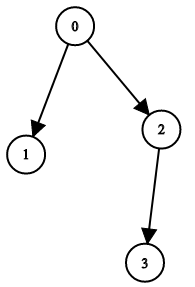
输入:n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
输出:true示例 2:

输入:n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
输出:false示例 3:

输入:n = 2, leftChild = [1,0], rightChild = [-1,-1]
输出:false示例 4:
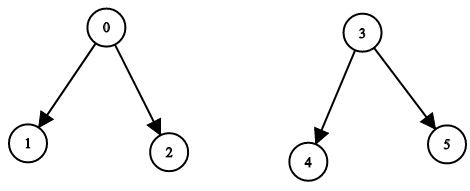
输入:n = 6, leftChild = [1,-1,-1,4,-1,-1], rightChild = [2,-1,-1,5,-1,-1]
输出:false提示:
1 <= n <= 10^4leftChild.length == rightChild.length == n-1 <= leftChild[i], rightChild[i] <= n - 1
函数签名:
func validateBinaryTreeNodes(cnt int, leftChild []int, rightChild []int) bool分析
给定的数据可能是一片森林,或者有环。需要把这两种情况排除。
1. 确定根节点
遍历一遍给定的两个数组,看看哪个节点不存在。
如若所有节点都存在,必有环,直接返回false;
如果不存在的节点多于一个,是一片森林,或者所有节点联通,但是根有多个(如M形),直接返回false;如果只找到了一个点不存在于给定的两个数组,是不是意味着就一定能构成一棵树呢?不一定,看下边的例子:
[1, -1, 3, 2]
[-1, -1, -1, -1]数组唯一缺失的点是 0,对应的树如下:
0 -> 1
2 <-> 3显然,这不是一棵合法的树,既是森林,也有环。
所以还需要第二步,从找到的根节点遍历得到答案。
2. 遍历
从找到的根节点开始,用染色的方法来确定是否能构建一棵树:
用一个数组 memo 来记录每个节点的状态,0 表示没有染色,1 表示染过色了且以该节点为根能构建一棵树,-1 表示染过色了且以该节点为根不能构建一棵树,比如步骤1的举例中节点2或3就不行。
最后,检查一遍 memo 数组,确保所有节点都染色了,实际上都需要染成色1,可以考虑步骤1举的那个例子,最后节点2、3将不会染色。
var n int
var memo, lefts, rights []int
func validateBinaryTreeNodes(cnt int, leftChild []int, rightChild []int) bool {
n = cnt
lefts, rights = leftChild, rightChild
if len(lefts) != n || len(rights) != n {
return false
}
root, ok := findRoot()
if !ok {
return false
}
memo = make([]int, n)
var mark func(i int) bool
mark = func(i int) bool {
if i == -1 { // 空节点
return true
}
if isMarked(i) {
return memo[i] == 1
}
if isMarked(lefts[i]) || isMarked(rights[i]) { // 有环
return false
}
memo[i] = -1
if mark(lefts[i]) && mark(rights[i]) {
memo[i] = 1
}
return memo[i] == 1
}
return mark(root) && allMarked()
}
func findRoot() (int, bool) {
set := make([]bool, n)
for i := 0; i < n; i++ {
l, r := lefts[i], rights[i]
if !isValid(l) || !isValid(r) {
return 0, false
}
if l != -1 {
set[l] = true
}
if r != -1 {
set[r] = true
}
}
root := -1
for i, ok := range set {
if ok {
continue
}
if root != -1 { // 至少有两个根节点,这是森林
return 0, false
}
root = i
}
if root == -1 { // 所有节点都在,必有环
return 0, false
}
return root, true
}
func isValid(node int) bool {
return node >= -1 && node < n
}
func isMarked(node int) bool {
return node != -1 && memo[node] != 0
}
func allMarked() bool {
for _, v := range memo {
if v == 0 {
return false
}
}
return true
}