987. 二叉树的垂序遍历
987. 二叉树的垂序遍历
难度困难
给你二叉树的根结点 root ,按 垂序遍历 返回其结点值。
对位于 (x, y) 的每个结点而言,其左右子结点分别位于 (x - 1, y - 1) 和 (x + 1, y - 1) 。
二叉树 垂序遍历 是由从左到右每个唯一 x 坐标的非空 报告 形成的列表,报告 是一个包含给定 x 坐标下所有节点的列表,其中节点需要按 y 坐标从最高到最低排序。如果 报告 中任意两个节点的 y 坐标相同,则值较小的节点应排在前面。
示例 1:
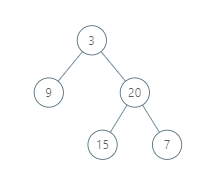
输入:root = [3,9,20,null,null,15,7]
输出:[[9],[3,15],[20],[7]]
解释:
在不丧失其普遍性的情况下,我们可以假设根结点位于 (0, 0):
然后,值为 9 的结点出现在 (-1, -1);
值为 3 和 15 的两个结点分别出现在 (0, 0) 和 (0, -2);
值为 20 的结点出现在 (1, -1);
值为 7 的结点出现在 (2, -2)。示例 2:
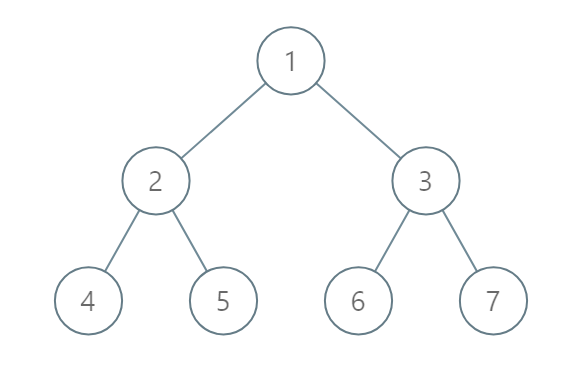
输入:root = [1,2,3,4,5,6,7]
输出:[[4],[2],[1,5,6],[3],[7]]
解释:
根据给定的方案,值为 5 和 6 的两个结点出现在同一位置。
然而,在报告 "[1,5,6]" 中,结点值 5 排在前面,因为 5 小于 6。提示:
- 树中结点数目总数在范围
[1, 1000]内 0 <= Node.val <= 1000
二叉树定义:
type TreeNode struct {
Val int
Left *TreeNode
Right *TreeNode
}函数签名:
func verticalTraversal(root *TreeNode) [][]int分析
二叉树的数据结构,DFS 的先、中、后序遍历最容易,借助队列等集合做 BFS 的层次遍历也可以,像这个问题里垂直遍历非常不直观。
需要借助数组、哈希表等数据结构来转化问题。比如一个思路是这样:
好在题目已经给出了一个方法,来确定每个节点的位置,就是给节点编号。可以把二叉树放到一个二维网格里,每个节点的位置用行号、列号标识,正好符合题目给的编号规则。
现在开始遍历树,不妨用先序遍历,看完整个过程就知道了用先序的原因。借助一个哈希表,在遍历 过程中,记录每一列出现的节点信息,包括节点值和其位置信息,因为列号已经作为哈希表的键,那么哈希表的值需要包含行号和节点值信息。当然,同一列会有多个行,甚至同列同行也会有重叠的节点,这样每列记录的节点会有多个,哈希表的值实际为一个数组,数组元素记录行号和节点值,可以定义一个结构体。
最后只需要按列一一构造结果即可。
注意,每列的元素,首先要按照行号升序排序,其次如果行号相同,要按照节点值升序排序。
// 用于记录节点所在行号和节点值的结构体
type Item struct {
row, val int
}
func verticalTraversal(root *TreeNode) [][]int {
var minC, maxC, maxR int // 需要知道行、列的上下左右边界,注意列可以是负数,行从0开始
cache := map[int][]Item{}
var dfs func(root *TreeNode, r, c int)
dfs = func(root *TreeNode, r, c int) {
if root == nil {
return
}
minC = min(minC, c)
maxC = max(maxC, c)
maxR = max(maxR, r)
cache[c] = append(cache[c], Item{row: r, val: root.Val})
dfs(root.Left, r+1, c-1)
dfs(root.Right, r+1, c+1)
}
dfs(root, 0, 0)
res := make([][]int, 0, len(cache))
for c := minC; c <= maxC; c++ {
parse(c, cache, &res)
}
return res
}
func parse(c int, cache map[int][]Item, res *[][]int) {
items, ok := cache[c]
if !ok {
return
}
sort.Slice(items, func(i, j int) bool {
if items[i].row == items[j].row {
return items[i].val < items[j].val
}
return items[i].row < items[j].row
})
tmp := make([]int, len(items))
for i := range tmp {
tmp[i] = items[i].val
}
*res = append(*res, tmp)
}